Exploring Computers: Tiny Assembler February 27, 2015

Ever wanted to write an assembler? If yes, this challenge from r/dailyprogrammer might interest you:

Tiny, a very simple fictional computer architecture, is programmed by an assembly language that has 16 mnemonics, with 37 unique op-codes. The system is based on Harvard architecture, and is very straight-forward: program memory is different from working memory, the machine only executes one instruction at a time, memory is an array of bytes from index 0 to index 255 (inclusive), and doesn’t have any relative addressing modes.
Your goal will be to write an assembler for Tiny: though you don’t need to simulate the code or machine components, you must take given assembly-language source code and produce a list of hex op-codes. You are essentially writing code that converts the lowest human-readable language to machine-readable language!

If that sounds exciting to you, feel free to shelve this article and go solve the challenge. I won’t discuss my solution here but will rather talk about what we can learn about computer architecture and assembly programming.

Tiny Architecture

So let’s have a closer look at this Tiny machine. First we learn that it’s based on the Harvard architecture. To grasp the implications, we’ll have to step back a bit. If we strip away all non-essential components from your computer, we’ll be left with two things: This is reminiscent of the Turing machine, a hypothetical device which describes computation in a similar fashion: It consists of an infinitely large tape, a reading/writing head and a bunch of rules that describe the its behaviour.the CPU and the memory. There are two popular strategies how to connect these two:

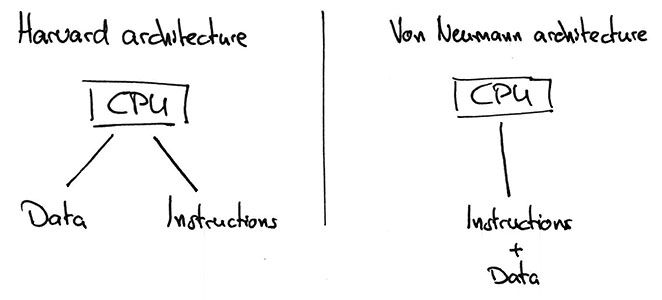
As you can see, the Harvard architectures separates between instruction memory and data memory. If you think about the early days of computing, this idea makes sense: Program instructions were stored on punch cards which were physically separate from working memory. Actually, Tiny might be such a machine, who knows?

The Harvard architecture’s advantage over the Von Neumann architecture is the ability to fetch code and data simultaneously. But then, it cannot treat code as data (which may be useful for things like Just-in-time compilation). Either way, modern architectures incorporate ideas from both Havard and Von Neumann architecture (for example the Modified Harvard architecture).

Let’s move on! The next fact is that Tiny only executes one instruction at a time. This refers to a technique called pipelining. It allows CPUs to process multiple instructions in parallel akin to assembly lines where multiple tasks are executed at the same time in order to maximize throughput. My computer’s CPU for example has a Source: Wikipedia: Ivy Bridge (microarchitecture).14- to 19-stage pipeline. Tiny on the other hand doesn’t have pipelining which simplifies the overall design.

After the description of the CPU architecture we now learn about the assembler code Tiny understands. The challenge description states that there are no relative addressing modes. This basically means that instructions have two argument types (immediate values and addresses) which again simplifies the design. Modern architectures on the other hand allow more nifty addressing modes like relative or indirect addressing.

Finally the description includes the supported instruction set. It lists 16 menmonics and Most instructions have multiple opcodes because they can take different types of arguments. For example the undefined instruction can either take a literal value or an address.37 opcodes. For comparison: Intel’s x86 instruction set reference lists more than 400 mnemonics alone. Compared with that, the Tiny instruction set is very ... you know ... tiny. And indeed, many useful instructions are missing. There is no multiplication or division built in, let alone support for I’ve tried to implement float point numbers for Tiny, but ran into problems because the source became so big that jumps got messed up due to integer overflows.float point processing. While it is possible to work around these issues, it makes writing more sophisticated programs harder.

Now that we have a basic understanding of how Tiny looks like, wouldn’t it be interesting to build a virtual machine for it?

Tiny VM

Building a virtual machine to emulate Tiny isn’t particularly complicated. Actually, all we have to do is to implement the instruction cycle:

1. Instruction fetch: Fetch the next instruction to execute.
2. Instruction decode: Decode the instruction and look up the expected operands. Then load the arguments from main memory.
3. Execute: Perform the requested operation.
4. Store results: Write the results of the operation back to main memory. If requested, update the instruction pointer.

One way or another, this instruction cycle is the foundation of any computer. So our VM’s main loop is just an implementation of this cycle in software. This of course requires some surrounding machinery – mainly for decoding the instruction and executing it – but the core idea remains simple.

If you’re curious, you can take a look at my Rust implementation of the Tiny VM (my original submission to r/dailyprogrammer is written in Python but its source code is rather messy, so I recommend checking out the Rust version :)

Approximating $\pi$

With the VM in place, can we actually do something interesting given the limitations of the architeture and instruction set? Turns out we can approximate $\pi$! Well, sort of. The lack of floating point support prevents us from actually calculating a decimal approximation. Instead, with the right algorithm we can compute a fractional number like $78\cdot \frac{4}{100}$.

Turns out the so-called dart board algorithm fills the bill. It’s a Monte Carlo algorithm which means it uses randomness and isn’t guaranteed to return a correct result. Instead, this algorithm offers an approximation to $\pi$. Without going into detail, the basic idea is to draw a quadrant inscribed in a square and then randomly throw “darts” at it. The ratio of darts that landed inside the circle to total darts will be Source: Jörg Arndt and Christoph Haenel: Pi Unleashed (Berlin: Springer-Verlag, 2006), 39-40.approximately equal to $\pi/4$.

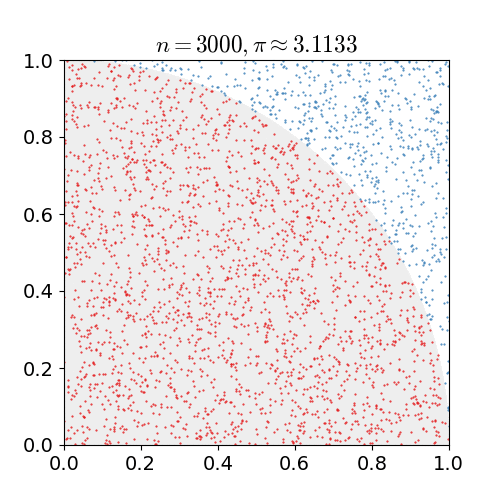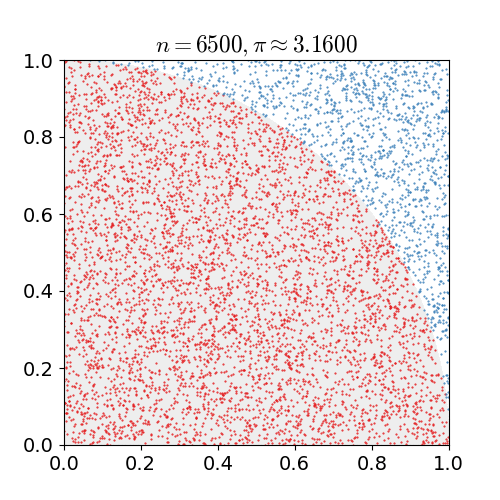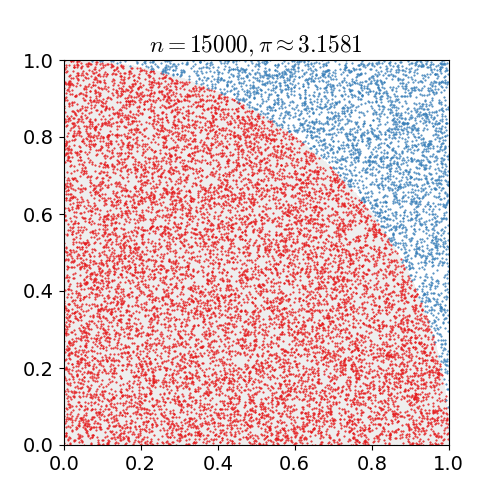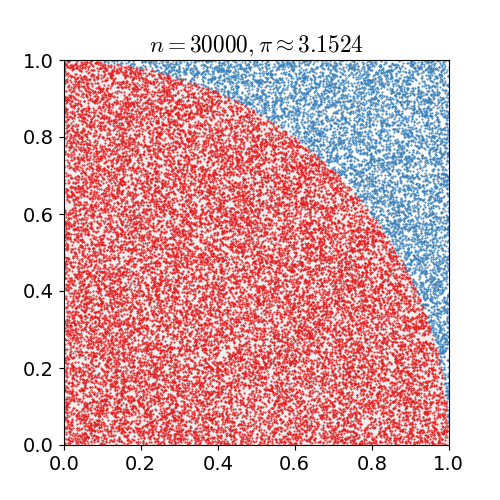
Implementing this algorithm requires a random number generator which Tiny luckily provides. We’ll still have to roll our own multiplication (and division for that matter), but the rest of the implementation is straight forward: We throw darts in a for loop, square the $x$ and $y$ coordinates, add them up and check whether the dart hit the circle. If that’s the case, we increment a counter. In the end, the final program is just 53 instructions long. What’s left is to assemble and run it!

The decimal value of $77 \cdot \frac{4}{100}$ is $3.08$ which I find close enough to $\pi$ to More runs of the program yield similar results: $2.96, 3.0, 3.28 \ldots$call this program a success!

Further reading

As always, here are some resources worth checking out:

• r/dailyprogrammer: Challenge #132 [Intermediate] Tiny Assembler: The original challange along with solutions in all kinds of languages.
• jverkamp.com: A ’Tiny’ virtual machine in Racket: A detailed explanation of a Tiny VM implementation in Racket along with a proof that Tiny is Touring complete.